Este é um guest post (artigo convidado) sobre a aplicação dos Números Complexos na Construção Civil. Foi escrito e enviado por Sebastião Vieira do Nascimento (Sebá). Professor Titular (por concurso) aposentado da UFCG – PB.
Este trabalho objetiva mostrar que os números complexos, como muitos imaginam, não são aplicados apenas em engenharia elétrica, mas sim, em problemas que envolvem a soma de dois quadrados.
José era filho de um agricultor e frequentava a escola do Ensino Médio. Certo dia o professor passou uma tarefa para casa sobre números complexos. Assim que José chega em casa, sua mãe pergunta:
– Qual o dever de casa, meu filho?
José responde:
– Uma lista de exercícios sobre números complexos. O pai de José ao ouvir falar em
números complexos, pergunta ao filho:
– E para que serve meu filho, na vida real, números complexos? O filho responde:
– Eu fiz a mesma pergunta ao professor, e ele me respondeu que a gente só veria a aplicação dos números complexos, caso a gente no futuro fizesse um curso de graduação em engenharia elétrica.
– É por isso, meu filho, que na época que estudei o Ensino Médio (antigo científico), nunca
tive o menor interesse em aprender esse tal de números complexos.
– Por que papai?
– Ora, porque durante o período que freqüente o Científico, em momento algum tive a oportunidade de ver, em sala de aula, uma só aplicação da matemática "ensinada" numa situação prática do dia a dia.
Certo dia o pai de José encontra com um professor por nome Sebá e pergunta-lhe:
– Professor, sou agricultor e meu filho estuda o Ensino Médio; o professor dele passou uma lista de exercícios sobre números complexos e disse que os números complexos só têm aplicação em curso de graduação de engenharia elétrica, isso é verdade?
Respondeu o professor Sebá:
Seja $N$ a área a ser dividida. Como o Sr. Antônio quer dividir a área $N$ em duas áreas quadradas, logo, $N=x^{2}+y^{2}$, onde $x$ e $y$ são inteiros positivos, ou seja, o zero não está incluído.
 Há dois casos a se considerar:
Há dois casos a se considerar:
a) $N>2$ um número natural primo;
b) $N>2$ um número natural composto.
a) Fermat descobriu, e provou, que há dois tipos de números primos: primos da forma $4x + 1$ e primos da forma $4x + 3$. Os primos da forma $4x + 1$ podem ser escritos como soma de dois quadrados de inteiros positivos de uma única maneira; já os primos da forma $4x + 3$, não podem ser escritos como soma de dois quadrados de inteiros positivos.
Regra de Sebá para escrever um número primo ($p$) da forma $4x + 1$ como soma de dois quadrados de inteiros positivos.
Se $p=x^{2}+y^{2}$ , então, como $p$ é ímpar, se $x$ for ímpar, $y$ será par; e se $x$ for par, $y$ será ímpar.
Vamos supor que $x$ seja par.
Como o último algarismo de um número primo pode ser $1$, $3$, $7$ ou $9$, logo:
a) Se o último algarismo de um primo da forma $4x + 1$ for $1$, testar $x$ terminado em $0$, $4$ e $6$;
b) Se o último algarismo de um primo da forma $4x + 1$ for $3$, testar $x$ terminado em $2$ e $8$;
c) Se o último algarismo de um primo da forma $4x + 1$ for $7$, testar $x$ terminado em $4$ e $6$;
d) Se o último algarismo de um primo da forma $4x + 1$ for $9$, testar $x$ terminado em $0$, $2$ e $8$.
Já que $p=x^{2}+y^{2}$, logo, $y=\sqrt{p-x^{2}}$.
Vá subtraindo $x^{2}$ de $p$; quando $p-x^{2}$ for um quadrado perfeito, pare, esse é o valor de $y$.
Exemplos:
01) Sabendo-se que 89 é um número primo, pode-se escrever 89 como soma de dois quadrados de inteiros positivos?
Resolução:
Como $89-1$ é divisível por $4$, logo, $89$ é um primo da forma $4x + 1$.
Já que $\sqrt{89}=9,43$ [Parte inteira (PI) 9]. Como $x$ é par, vamos considerar $PI=8$.
Como $p=89$ termina com o algarismo $9$, pela regra de Sebá, basta testar os números pares menores ou igual a $8$ terminados em $0$, $2$ e $8$. Como $10>8$, logo, basta testar: $x = 2$ e $8$.
$89-2^{2}=85$ [Não é quadrado perfeito (NQP)]
$89-8^{2}=25$ [É quadrado perfeito (QP)]
Portanto, $89=8^{2}+5^{2}$.
02) Sabendo-se que $241$ é um número primo, pode-se escrever $241$ como soma de dois quadrados de inteiros positivos?
Resolução:
Como $241-1$ é divisível por $4$, logo, $241$ é um primo da forma $4x + 1$.
Já que $\sqrt{241}=15,52$ . [Parte inteira (PI) 15]. Como $x$ é par, vamos considerar $PI = 14$. Como $p = 241$ termina com o algarismo $1$, pela regra de Sebá, basta testar os números pares menores ou igual a $14$ terminados em $0$, $4$ e $6$. Como $20>14$, logo, basta testar: $x = 10$, $4$, $14$ e $6$.
$241-10^{2}=141$ (NQP)
$241-4^{2}=225$ (QP)
Portanto, $241=15^{2}+4^{2}$.
03) Sabendo-se que $317$ é um número primo, pode-se escrever $317$ como soma de dois quadrados de inteiros positivos?
Resolução:
Como $317-1$ é divisível por $4$, logo, $317$ é um primo da forma $4x + 1$.
Já que $\sqrt{317}=17,8$ . [Parte inteira (PI) 17]. Como $x$ é par, vamos considerar $PI = 16$. Como $p = 317$ termina com o algarismo $7$, pela regra de Sebá, basta testar os números pares menores ou igual a $16$ terminados em $4$ e $6$. Logo, basta testar: $x = 4$, $14$, $6$ e $16$.
$317-4^{2}=301$ (NQP)
$317-14^{2}=121$ (QP)
Portanto, $317=14^{2}+11^{2}$.
04) Sabendo-se que $613$ é um número primo, pode-se escrever $613$ como soma de dois quadrados de inteiros positivos?
Resolução:
Como $613-1$ é divisível por $4$, logo, $613$ é um primo da forma $4x + 1$.
Já que $\sqrt{613}=24,7$ . [Parte inteira (PI) 24]. Como $x$ é par, vamos considerar $PI = 24$. Como $p = 613$ termina com o algarismo $3$, pela regra de Sebá, basta testar os números pares menores do que $24$ terminados em $2$ e $8$. Logo, basta testar: $x = 2$, $12$, $22$, $8$ e $18$.
$613-2^{2}=609$ (NQP)
$613-18^{2}=289$ (QP)
Portanto, $613=18^{2}+17^{2}$.
b) Segundo Fermat, um número natural composto $N$ é a soma de dois quadrados de inteiros positivos se e somente se todo divisor primo de $N$ da forma $4k + 3$ aparecer com o expoente par na fatoração de $N$ como produto de primos.
Como todo número composto pode ser decomposto em fatores primos, logo, segundo Fermat, se na decomposição de um número composto existir um primo da forma $4x + 3$ com expoente ímpar, esse composto não pode ser escrito como soma de dois quadrados de inteiros positivos.
Exemplos de compostos que podem ser escritos como soma de dois quadrados de inteiros positivos:
$18 = 3 \cdot 3 \cdot 2 = 3^{2} \cdot 2$. Os fatores primos de $18$ são $3$ e $2$, o expoente de $3$ é par e $2$ pode ser escrito como soma de dois quadrados de inteiros positivos.
$18 = 3^{2}\cdot (1^{2} + 1^{2}) = 3^{2} + 3^{2}$.
$45 = 3 \cdot 3 \cdot 5 = 3^{2} \cdot 5$. Os fatores primos de $45$ são $3$ e $5$, o expoente de $3$ é par e $5$ pode ser escrito como soma de dois quadrados de inteiros positivos.
$45=3^{2} \cdot (2^{2} + 1^{2}) = 6^{2} + 3^{2}$.
$490 = 7 \cdot 7 \cdot 5 \cdot 2 = 7^{2} \cdot 10$. Os fatores primos de $490$ são $7$, $5$ e $2$, o expoente de $7$ é par e $10$ pode ser escrito como soma de dois quadrados de inteiros positivos.
$490 = 7^{2} \cdot (3^{2} + 1^{2} ) = 21^{2} + 7^{2}$.
E assim por diante.
Exemplos de compostos que não podem ser escritos como soma de dois quadrados de inteiros positivos:
$6 = 3 \cdot 2$ (Os fatores primos de $6$ são $3$ e $2$, mas o expoente de $3$ é impar)
$15 = 3 \cdot 5$ (Os fatores primos de $15$ são $3$ e $5$, mas o expoente de $3$ é ímpar)
$3773 = 7 \cdot 7 \cdot 7 \cdot 11 = 7^{3} \cdot 11$ (Os fatores primos de $3773$ são $7$ e $11$, mas o expoente de $7$ é impar)
$135 = 3 \cdot 3 \cdot 3 \cdot 5 = 3^{3} \cdot 5$ (Os fatores primos de $135$ são $3$ e $5$, mas o expoente de $3$ é impar)
E assim por diante.
Vamos usar números complexos para escrever $260$ como soma de dois quadrados de inteiros positivos.
$260 = 20 \cdot 13 = (2^{2} + 4^{2} ) \cdot (2^{2} + 3^{2})$
Escrevendo $2^{2} + 4^{2}$ e $2^{2} + 3^{2}$ como dois números complexos, obtém-se: $2 + 4i$ e $2 + 3i$.
Multiplicando os dois números complexos, obtém-se:
$(2 + 4i) \cdot (2 + 3i) = – 8 + 14i$
Como queremos escrever $260$ como soma de dois quadrados de inteiros positivos, então, $260 = 14^{2} + 8^{2}$.

Resposta: A casa deve ter uma área de $196$ $m^{2}$ e o depósito uma área de $64$ $m^{2}$.
Multiplicando um dos números complexos $2 + 4i$ ou $2 + 3i$ pelo seu conjugado obtém-se:
$(2 – 4i) \cdot (2 + 3i) = 16 – 2i$.
Como queremos escrever $260$ como soma de dois quadrados de inteiros positivos, então, $260 = 16^{2} + 2^{2}$.
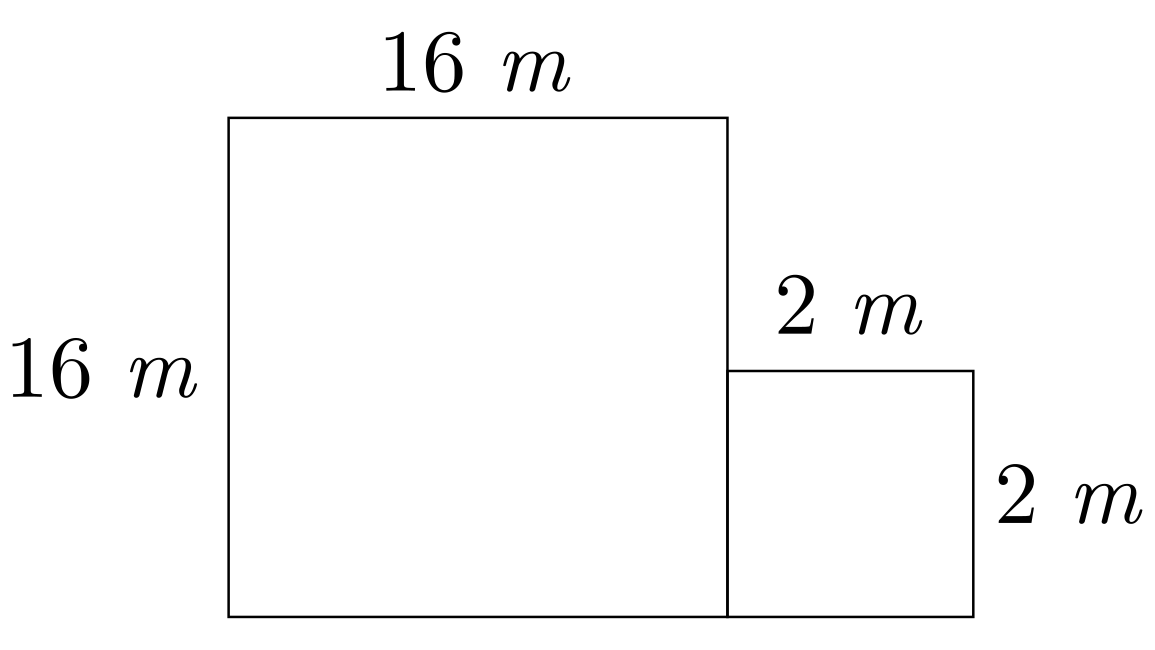
Resposta: A casa deve ter uma área de $256$ $m^{2}$ e o depósito uma área de $4$ $m^{2}$.
Mais artigos desse autor Envie um artigo Ajude o blog
José era filho de um agricultor e frequentava a escola do Ensino Médio. Certo dia o professor passou uma tarefa para casa sobre números complexos. Assim que José chega em casa, sua mãe pergunta:
– Qual o dever de casa, meu filho?
José responde:
– Uma lista de exercícios sobre números complexos. O pai de José ao ouvir falar em
números complexos, pergunta ao filho:
– E para que serve meu filho, na vida real, números complexos? O filho responde:
– Eu fiz a mesma pergunta ao professor, e ele me respondeu que a gente só veria a aplicação dos números complexos, caso a gente no futuro fizesse um curso de graduação em engenharia elétrica.
– É por isso, meu filho, que na época que estudei o Ensino Médio (antigo científico), nunca
tive o menor interesse em aprender esse tal de números complexos.
– Por que papai?
– Ora, porque durante o período que freqüente o Científico, em momento algum tive a oportunidade de ver, em sala de aula, uma só aplicação da matemática "ensinada" numa situação prática do dia a dia.
Certo dia o pai de José encontra com um professor por nome Sebá e pergunta-lhe:
– Professor, sou agricultor e meu filho estuda o Ensino Médio; o professor dele passou uma lista de exercícios sobre números complexos e disse que os números complexos só têm aplicação em curso de graduação de engenharia elétrica, isso é verdade?
Respondeu o professor Sebá:
– Não! Vejamos um flagrante da vida real
O Sr. Manoel tem um terreno retangular com $260$ metros quadrados e deseja dividir esse terreno em dois terrenos quadrados; o maior terreno é para construir uma casa e o outro para construir um depósito para os trabalhadores guardarem seus instrumentos de trabalho, pergunta-se: que área deve ter a casa? E o depósito deve ter que área?Seja $N$ a área a ser dividida. Como o Sr. Antônio quer dividir a área $N$ em duas áreas quadradas, logo, $N=x^{2}+y^{2}$, onde $x$ e $y$ são inteiros positivos, ou seja, o zero não está incluído.

a) $N>2$ um número natural primo;
b) $N>2$ um número natural composto.
a) Fermat descobriu, e provou, que há dois tipos de números primos: primos da forma $4x + 1$ e primos da forma $4x + 3$. Os primos da forma $4x + 1$ podem ser escritos como soma de dois quadrados de inteiros positivos de uma única maneira; já os primos da forma $4x + 3$, não podem ser escritos como soma de dois quadrados de inteiros positivos.
Regra de Sebá para escrever um número primo ($p$) da forma $4x + 1$ como soma de dois quadrados de inteiros positivos.
Se $p=x^{2}+y^{2}$ , então, como $p$ é ímpar, se $x$ for ímpar, $y$ será par; e se $x$ for par, $y$ será ímpar.
Vamos supor que $x$ seja par.
Como o último algarismo de um número primo pode ser $1$, $3$, $7$ ou $9$, logo:
a) Se o último algarismo de um primo da forma $4x + 1$ for $1$, testar $x$ terminado em $0$, $4$ e $6$;
b) Se o último algarismo de um primo da forma $4x + 1$ for $3$, testar $x$ terminado em $2$ e $8$;
c) Se o último algarismo de um primo da forma $4x + 1$ for $7$, testar $x$ terminado em $4$ e $6$;
d) Se o último algarismo de um primo da forma $4x + 1$ for $9$, testar $x$ terminado em $0$, $2$ e $8$.
Já que $p=x^{2}+y^{2}$, logo, $y=\sqrt{p-x^{2}}$.
Vá subtraindo $x^{2}$ de $p$; quando $p-x^{2}$ for um quadrado perfeito, pare, esse é o valor de $y$.
Exemplos:
01) Sabendo-se que 89 é um número primo, pode-se escrever 89 como soma de dois quadrados de inteiros positivos?
Resolução:
Como $89-1$ é divisível por $4$, logo, $89$ é um primo da forma $4x + 1$.
Já que $\sqrt{89}=9,43$ [Parte inteira (PI) 9]. Como $x$ é par, vamos considerar $PI=8$.
Como $p=89$ termina com o algarismo $9$, pela regra de Sebá, basta testar os números pares menores ou igual a $8$ terminados em $0$, $2$ e $8$. Como $10>8$, logo, basta testar: $x = 2$ e $8$.
$89-2^{2}=85$ [Não é quadrado perfeito (NQP)]
$89-8^{2}=25$ [É quadrado perfeito (QP)]
Portanto, $89=8^{2}+5^{2}$.
02) Sabendo-se que $241$ é um número primo, pode-se escrever $241$ como soma de dois quadrados de inteiros positivos?
Resolução:
Como $241-1$ é divisível por $4$, logo, $241$ é um primo da forma $4x + 1$.
Já que $\sqrt{241}=15,52$ . [Parte inteira (PI) 15]. Como $x$ é par, vamos considerar $PI = 14$. Como $p = 241$ termina com o algarismo $1$, pela regra de Sebá, basta testar os números pares menores ou igual a $14$ terminados em $0$, $4$ e $6$. Como $20>14$, logo, basta testar: $x = 10$, $4$, $14$ e $6$.
$241-10^{2}=141$ (NQP)
$241-4^{2}=225$ (QP)
Portanto, $241=15^{2}+4^{2}$.
03) Sabendo-se que $317$ é um número primo, pode-se escrever $317$ como soma de dois quadrados de inteiros positivos?
Resolução:
Como $317-1$ é divisível por $4$, logo, $317$ é um primo da forma $4x + 1$.
Já que $\sqrt{317}=17,8$ . [Parte inteira (PI) 17]. Como $x$ é par, vamos considerar $PI = 16$. Como $p = 317$ termina com o algarismo $7$, pela regra de Sebá, basta testar os números pares menores ou igual a $16$ terminados em $4$ e $6$. Logo, basta testar: $x = 4$, $14$, $6$ e $16$.
$317-4^{2}=301$ (NQP)
$317-14^{2}=121$ (QP)
Portanto, $317=14^{2}+11^{2}$.
04) Sabendo-se que $613$ é um número primo, pode-se escrever $613$ como soma de dois quadrados de inteiros positivos?
Resolução:
Como $613-1$ é divisível por $4$, logo, $613$ é um primo da forma $4x + 1$.
Já que $\sqrt{613}=24,7$ . [Parte inteira (PI) 24]. Como $x$ é par, vamos considerar $PI = 24$. Como $p = 613$ termina com o algarismo $3$, pela regra de Sebá, basta testar os números pares menores do que $24$ terminados em $2$ e $8$. Logo, basta testar: $x = 2$, $12$, $22$, $8$ e $18$.
$613-2^{2}=609$ (NQP)
$613-18^{2}=289$ (QP)
Portanto, $613=18^{2}+17^{2}$.
b) Segundo Fermat, um número natural composto $N$ é a soma de dois quadrados de inteiros positivos se e somente se todo divisor primo de $N$ da forma $4k + 3$ aparecer com o expoente par na fatoração de $N$ como produto de primos.
Como todo número composto pode ser decomposto em fatores primos, logo, segundo Fermat, se na decomposição de um número composto existir um primo da forma $4x + 3$ com expoente ímpar, esse composto não pode ser escrito como soma de dois quadrados de inteiros positivos.
Exemplos de compostos que podem ser escritos como soma de dois quadrados de inteiros positivos:
$18 = 3 \cdot 3 \cdot 2 = 3^{2} \cdot 2$. Os fatores primos de $18$ são $3$ e $2$, o expoente de $3$ é par e $2$ pode ser escrito como soma de dois quadrados de inteiros positivos.
$18 = 3^{2}\cdot (1^{2} + 1^{2}) = 3^{2} + 3^{2}$.
$45 = 3 \cdot 3 \cdot 5 = 3^{2} \cdot 5$. Os fatores primos de $45$ são $3$ e $5$, o expoente de $3$ é par e $5$ pode ser escrito como soma de dois quadrados de inteiros positivos.
$45=3^{2} \cdot (2^{2} + 1^{2}) = 6^{2} + 3^{2}$.
$490 = 7 \cdot 7 \cdot 5 \cdot 2 = 7^{2} \cdot 10$. Os fatores primos de $490$ são $7$, $5$ e $2$, o expoente de $7$ é par e $10$ pode ser escrito como soma de dois quadrados de inteiros positivos.
$490 = 7^{2} \cdot (3^{2} + 1^{2} ) = 21^{2} + 7^{2}$.
E assim por diante.
Exemplos de compostos que não podem ser escritos como soma de dois quadrados de inteiros positivos:
$6 = 3 \cdot 2$ (Os fatores primos de $6$ são $3$ e $2$, mas o expoente de $3$ é impar)
$15 = 3 \cdot 5$ (Os fatores primos de $15$ são $3$ e $5$, mas o expoente de $3$ é ímpar)
$3773 = 7 \cdot 7 \cdot 7 \cdot 11 = 7^{3} \cdot 11$ (Os fatores primos de $3773$ são $7$ e $11$, mas o expoente de $7$ é impar)
$135 = 3 \cdot 3 \cdot 3 \cdot 5 = 3^{3} \cdot 5$ (Os fatores primos de $135$ são $3$ e $5$, mas o expoente de $3$ é impar)
E assim por diante.
Vamos usar números complexos para escrever $260$ como soma de dois quadrados de inteiros positivos.
$260 = 20 \cdot 13 = (2^{2} + 4^{2} ) \cdot (2^{2} + 3^{2})$
Escrevendo $2^{2} + 4^{2}$ e $2^{2} + 3^{2}$ como dois números complexos, obtém-se: $2 + 4i$ e $2 + 3i$.
Multiplicando os dois números complexos, obtém-se:
$(2 + 4i) \cdot (2 + 3i) = – 8 + 14i$
Como queremos escrever $260$ como soma de dois quadrados de inteiros positivos, então, $260 = 14^{2} + 8^{2}$.

Resposta: A casa deve ter uma área de $196$ $m^{2}$ e o depósito uma área de $64$ $m^{2}$.
Multiplicando um dos números complexos $2 + 4i$ ou $2 + 3i$ pelo seu conjugado obtém-se:
$(2 – 4i) \cdot (2 + 3i) = 16 – 2i$.
Como queremos escrever $260$ como soma de dois quadrados de inteiros positivos, então, $260 = 16^{2} + 2^{2}$.

Resposta: A casa deve ter uma área de $256$ $m^{2}$ e o depósito uma área de $4$ $m^{2}$.
Conclusão:
Das duas respostas, o Sr. Manoel tem que escolher uma: construir uma casa com $256$ $m^{2}$ ou construir uma casa com $196$ $m^{2}$.
Este é um guest post (artigo convidado). Foi escrito e enviado por Sebastião Vieira do Nascimento (Sebá). Professor Titular (por concurso) aposentado da UFCG – PB.











Excelente artigo (como sempre).
ResponderExcluirValeu! Mas os créditos vão para o professor Sebastião.
ExcluirAbraço!