Dois flagrantes da vida real sobre Produto Notável

Para que serve realmente o produto notável sobre a Diferença de dois Quadrados?

Neste mês de maio foi publicado neste blog um artigo de autoria do professor Edigley Alexandre, concernente à seguinte pergunta feita por um de seus alunos: Professor, existe um jeito fácil de estudar Matemática?

Após comentar sobre a pergunta do aluno (Leia o artigo), o  professor Edigley faz a seguinte pergunta: se você perguntar para um aluno do 8º ano como calcular o valor de $1984^{2}-1983^{2}$, qual a primeira coisa que ele irá fazer?

  1. Calcular as potências, depois subtrair os resultados? De tanto repetir cálculos de potência ele acerta a questão, porém gastando certo tempo.
   2. Ou lembrar que  $A^{2}-B^{2}=(A+B) \cdot (A-B)$? Pura memorização?

Para que serve realmente o produto notável $A^{2}-B^{2}=(A+B) \cdot (A-B)$?

Parafraseando o professor A. P. Ricieri, talvez o caro leitor responda: se pensar nessa pergunta baseando-me naquilo que me “ensinaram” nas escolas “chatas” da vida, afirmaria: PARA NADA!

No entanto, pensando melhor sobre o assunto, responderia: PARA SER COBRADA NAS PROVAS!  Porém, meditando compenetradamente no tema, diria: TAÍ ALGO QUE REALMENTE NÃO SEI?

Não sei se o leitor (ou aluno) que está frequentando, ou aquele que já frequentou a escola do Ensino Fundamental, concorda com a resposta. Sinceramente, concordo. Concordo, porque durante o período que frequentei a escola do Ensino Fundamental (antigos primário e ginásio) em momento algum tive a oportunidade de ver, em sala de aula, uma só aplicação da matemática ensinada. 

Após muitos anos entrevistando pessoas dos setores agrícola, industrial e de serviços, pôde-se constatar que existem muitos problemas com os quais nos defrontamos no dia a dia que podem ser resolvidos com muitos assuntos de matemática vistos no Ensino Fundamental. E por meio dessas entrevistas chegou-se às seguintes conclusões:

a) a aversão que o aluno tem à matemática, decorre da distância que o Ensino Fundamental guarda da realidade em que vive;

b) já que o aluno não consegue fazer a conexão entre o que aprende e suas necessidades do dia a dia, daí vem o desinteresse e, em consequência, a versão à matemática;

c) toda a matemática do Ensino Fundamental é importante para a vida do aluno, mas da forma como é “ensinada” não serve para nada.

Para que ensinar o produto notável, somente pelo fato de esse assunto fazer parte do currículo do Ministério da Educação? Para mim é coisa que, isolada, não significa absolutamente nada. Pior: atrapalha a carreira de muitos jovens.

Como podemos esperar algum resultado do ensino da matemática, se cujas ementas não mencionam aplicações? Ou será que o que consta nas ementas é apenas para ser cobrado nas provas?

Como seria estimulante, para todos os alunos, se o professor mostrasse o quanto é poderoso e fundamental aquilo que estão aprendendo!

Os sistemas educacionais, principalmente os de matemática, têm sido, nos últimos duzentos anos, dominados pelo que se pode chamar uma fascinação pelo teórico e abstrato. Teorias e técnicas são muitas vezes apresentadas e desenvolvidas sem relacionamento com fatos reais e, mesmo quando são ilustradas com exemplos, apresentam-se de maneira artificial.

Fica-se no teórico e abstrato, mencionando que “essas teorias e técnicas servem para isso ou aquilo”, ilustrando com exemplos artificiais, manipulados e descontextualizados. 

Dois flagrantes da vida real sobre Produto Notável

Esses dois flagrantes da vida real necessitará da compreensão sobre um teorema. Ele foi extraído de um livro de teoria dos números.

Teorema 1: Um número inteiro n pode ser escrito como a diferença de dois quadrados de inteiros, $n=x^{2}- y^{2}$, se e somente se $n$ é ímpar ou múltiplo de $4$.

Demonstração do mesmo livro:

Uma forma direta de obter a representação de n como diferença de dois quadrados é a seguinte:

Se $n$ é múltiplo de $4$:

$n=4k=(k+1)^{2}-(k-1)^{2}$

Se $n$ é ímpar:

$n=2k+1=(k+1)^{2}-k^{2}$

Teorema de Sebá:

Todo número ímpar (I), maior que a unidade, pode ser escrito como diferença de dois quadrados de inteiros: $I=x^{2}-y^{2}$, de uma ou mais maneiras diferentes, por meio das duas equações:

$x=\cfrac{I+k^{2}}{2k}$ e $y=x-k$

Onde $k$ são os divisores de $I$, tal que $1 \leq k^{2}< I$.

Demonstração:

Como $I=x^{2}-y^{2}$, logo:

$x+y=\cfrac{I+k^{2}}{x-y}$

Como $x$ e $y$ são inteiros positivos, logo, $x-y$ são os divisores de I.

Se $x-y=k$, então:

$x+y=\cfrac{1}{k}$

Temos o seguinte sistema de equações:

$\left\{\begin{matrix} x-y=k & \\ x+y=\cfrac{1}{k} & \end{matrix}\right.$

Resolvendo-o, obtém-se:

$x=\cfrac{I+k^{2}}{2k}$ e $y=x-k$

Note que se $k^{2} \geq I$, implica $x-k \leq 0$, logo, $1 \leq k^{2} < I$.

Exemplo 1: De quantas maneiras diferentes pode-se escrever $121=x^{2}-y^{2}$?

Os divisores de $121$, tal que $1 \leq k^{2} < 121$, é: $1$. Logo, pode-se escrever $121=x^{2}-y^{2}$ de uma única maneira.

Para $k=1$ e $I=121$:

$x=\cfrac{121+1^{2}}{2 \cdot 1}=61$ e $y=61-1=60$

Assim:

$121=61^{2}-60^{2}$

Caso escolhêssemos $k=11$, teríamos $k^{2}=11^{2}=121=I$, e obter-se-ia:

$x=\cfrac{121+11^{2}}{2 \cdot 11}=11$ e $y=11-11=0$

Exemplo 2: De quantas maneiras diferentes pode-se escrever $13=x^{2}-y^{2}$?

Os divisores de $13$, tal que $1 \leq k^{2} < 13$, é: $1$. Logo, pode-se escrever $13=x^{2}-y^{2}$ de uma única maneira como a diferença de dois quadrados.

Para $k=1$ e $I=13$:

$x=\cfrac{13+1^{2}}{2 \cdot 1}=7$ e $y=7-1=6$

Assim:

$13=7^{2}-6^{2}$

Exemplo 3: De quantas maneiras diferentes pode-se escrever $117=x^{2}-y^{2}$?

Os divisores de $117$, tal que $1 \leq k^{2} < 117$, é: $1$, $3$ e $9$. Logo, temos três maneiras diferentes de escrever 117 como diferença de dois quadrados.

Modo 1: para $k=1$ e $I=117$:

$x=\cfrac{117+1^{2}}{2 \cdot 1}=59$ e $y=59-1=58$

Assim:

$117=59^{2}-58^{2}$

Modo 2: para $k=3$ e $I=117$:

$x=\cfrac{117+3^{2}}{2 \cdot 3}=21$ e $y=21-3=18$

Assim:

$117=21^{2}-18^{2}$

Modo 3: para $k=9$ e $I=117$:

$x=\cfrac{117+9^{2}}{2 \cdot 9}=11$ e $y=11-9=2$

Assim:

$117=11^{2}-2^{2}$

Caso escolhêssemos $k=13$, teríamos $k^{2}=13^{2}=169 > 117=I$, e obter-se-ia:

$x=\cfrac{117+13^{2}}{2 \cdot 13}=11$ e $y=11-13=-2$ (negativo)

Pelo teorema extraído de um livro de teoria dos números:

Se $n$ é ímpar:

$n=2k+1=(k+1)^{2}-k^{2}$

Se $n=117$, $k=58$, logo:

$117=(58+1)^{2}-58^{2}=59^{2}-58^{2}$

Conclusão:

Pelo teorema extraído de um livro de teoria dos números, $117$ só poderia ser escrito de uma única maneira como diferença de dois quadrados; já pelo Teorema de Sebá, o número 117 pode ser escrito de três maneiras diferentes como diferença de dois quadrados: $117=11^{2}-2^{2}=21^{2}-18^{2}=59^{2}-18^{2}$.

Flagrante da vida real 1

O Sr. Manoel tem um terreno com dimensão $10$ x $13$ e deseja construir uma casa com um depósito, internamente, anexo à casa para os trabalhadores guardarem seus instrumentos de trabalho; a área que sobrar será utilizada na criação de galinhas. Se ele deseja que a diferença entre a área da casa e a área do depósito seja $91$ $m²$, pergunta-se:

a) quantos metros quadrados tem as áreas do depósito e da casa?

b) quantos metros quadrados sobram dos $130$ $m²$?

Os divisores de $91$, tal que $1 \leq k^{2} < 91$, são: $1$ e $7$. De acordo com as fórmulas deduzidas acima, temos:

Para $k=1$:

$x=\cfrac{91+1}{2 \cdot 1}=46$ e $y=46-1=45$

$91=46^{2}-45^{2}$

$46^{2}=2116$ $m²$ e $45^{2}=2025$ $m²$

Essa solução só tem sentido matemático, haja vista que a dimensão do terreno do Sr. Manoel é $10m$ x $13m$ ou seja, $130$ $m²$ e a dimensão do depósito é $45m$ x $45m$, ou seja, $2025$ $m²$.

Para $k=7$:

$x=\cfrac{91+7^{2}}{2 \cdot 7}=10$ e $y=10-7=3$

$91=10^{2}-3^{2}$

$10^{2}=100$ $m²$ e $3^{2}=9$ $m²$

Respostas:

a) A área do depósito tem $9$ $m²$ e a da casa tem $100$ $m²$.

b) Sobraram $21$ $m²$.

Flagrante da vida real 2

José possui um terreno retangular cujas medidas são $60m$ x $110m$ e quer dividi-lo em lotes menores. Quer separar um lote de $X$ $m²$ para o cultivo de hortaliças e o restante quer dividi-lo em outros dois lotes quadrados para criar animais, de tal modo que a diferença entre esses dois lotes seja igual a $105$ $m²$. Pergunta-se:

a) Em quantas formas diferentes José pode dividir a parte de seu terreno destinada à criação de animais, obedecendo a suas exigências?

b) Quais as medidas de cada lote?

c) Quanto sobra de área do terreno para o cultivo de hortaliças para cada situação acima?

Resolução:

José quer dividir seu terreno em lotes menores seguindo uma lei matemática um tanto incomum. Podemos imaginar que José, no mínimo, é apreciador da Matemática.

Os divisores de $105$, tal que $1 \leq k^{2} < 105$, são: $1$, $3$, $5$ e $7$. De acordo com as fórmulas deduzidas acima, temos:

Para $k=1$ e $I=105$:

$x=\cfrac{105+1}{2 \cdot 1}=53$ e $y=53-1=52$

$105=53^{2}-52^{2}$

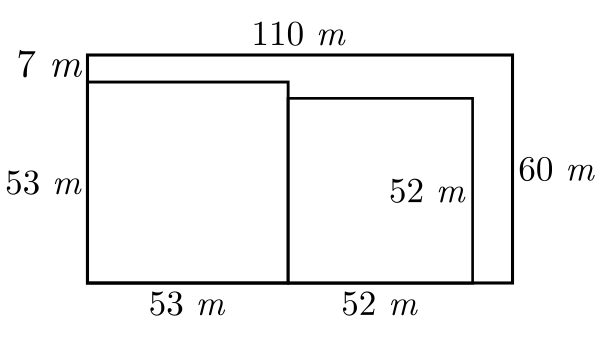FORMA 1:

Para $k=3$ e $I=105$:

$x=\cfrac{105+3^{2}}{2 \cdot 3}=19$ e $y=19-3=16$

$105=19^{2}-16^{2}$

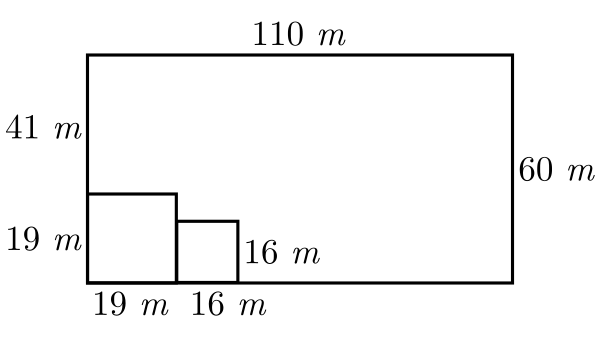FORMA 2:

Para $k=5$ e $I=105$:

$x=\cfrac{105+5^{2}}{2 \cdot 5}=13$ e $y=13-5=8$

$105=13^{2}-8^{2}$

FORMA 3:

Para $k=7$ e $I=105$:

$x=\cfrac{105+7^{2}}{2 \cdot 7}=11$ e $y=11-7=4$

$105=11^{2}-4^{2}$

FORMA 4:

Respostas:

a) José pode separar o terreno em quatro formas distintas.

b) As medidas dos lotes são:

Forma 1:

Lote 1 possui $53m$ x $53m = 2.809$ $m²$
Lote 2 possui $52m$ x $52m = 2.704$ $m²$

Forma 2:

Lote 1 possui $19m$ x $19m = 361$ $m²$
Lote 2 possui $16m$ x 16m = 256$ $m²$

Forma 3:

Lote 1 possui $13m$ x $13m = 169$ $m²$
Lote 2 possui $8m$ x $8m = 64$ $m²$

Forma 4:

Lote 1 possui $11m$ x $11m = 121$ $m²$
Lote 2 possui $4m$ x $4m = 16$ $m²$

c) O terreno de José possui medidas de $60m$ x $110m = 6.600$ $m²$ . Sendo assim, ao dividi-lo em lotes conforme as formas encontradas em b), temos que as áreas que sobram para o cultivo de hortaliças será:

Para forma 1:

$6600-(2809+2704)=1087$ $m²$

Para forma 2:

$6600-(361+256)=5983$ $m²$

Para forma 3:

$6600-(169+64)=6367$ $m²$

Para forma 4:

$6600-(121+16)=6463$ $m²$

Vemos que existem 4 formas diferentes de dividir o terreno em lotes, de modo a atender as exigências de José. Sendo assim, ele terá que decidir qual das quatro configurações é a melhor para aplicar em sua realidade.

Este é um guest post (artigo convidado). Foi escrito e enviado por Sebastião Vieira do Nascimento (Sebá). Professor Titular (por concurso) aposentado da UFCG – PB.

Mais artigos desse autor Envie um artigo Ajude o blog