Aprenda a fatorar equações e esqueça de Bhaskara!

Neste artigo você entenderá que para resolver equações do 2º grau, não precisa usar sempre a fórmula de Bhaskara.

Leia tudo antes de julgar pelo título.

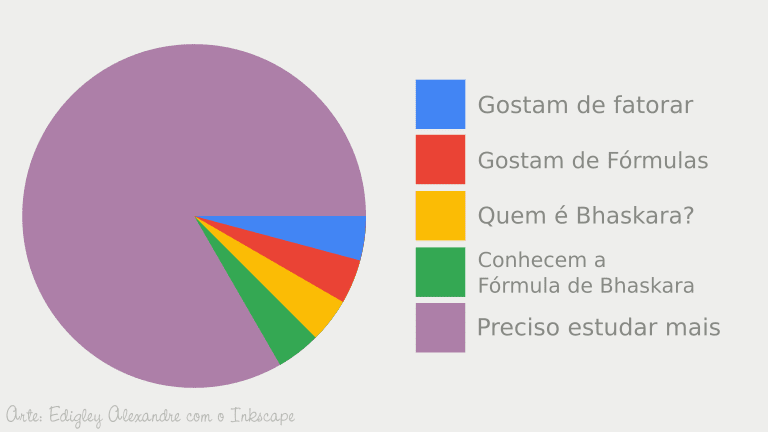
Faça uma pesquisa entre seus alunos com a seguinte pergunta: vocês preferem teoria matemática rigorosa (propriedades matemáticas) ou fórmulas matemáticas?

Essa pequena amostra apenas releva o quão ambas as perguntas (teoria matemática e fórmulas matemáticas) são objetos de uma série de fatores sobre o nível de aprendizagem matemático das pessoas. O motivo é que, por si só, o nome fórmula matemática já carrega uma fama nada boa, ainda que as mesmas pessoas que pensam assim, não saibam sobre propriedades matemáticas rigorosas.

Neste pensamento não tirarei a razão do aluno, que pergunta: professor, como encontrar a solução para essa equação do 2º grau? E o professor responde: use essa fórmula aqui!

Ensinar a pensar está em falta nas escolas. Culpar o sistema de ensino não adianta muito. Uma pequena contribuição faz muita diferença.

Neste artigo você entenderá que para resolver equações do 2º grau, não precisa usar sempre a fórmula de Bhaskara.

O que quero dizer com 'teoria matemática rigorosa'?

A Matemática é sustentada por diversos pilares. Eles são mais conhecidos como axiomas matemáticos. São "verdades" lógicas (ou até filosóficas) absolutas que garantem a existência de propriedades matemáticas aplicadas desde a Adição de números Naturais aos mais complexos temas matemáticos.

É uma sentença ou proposição que não é provada ou demonstrada e é considerada como óbvia ou como um consenso inicial necessário para a construção ou aceitação de uma teoria. Por essa razão, é aceita como verdade e serve como ponto inicial para dedução e inferências de outras verdades (dependentes de teoria).

Axiomas matemáticos em $\mathbb{R}$ (Reais):

• Associatividade: para quaisquer $x,y,z \in \mathbb{R}$ tem-se $(x+y)+z=x+(y+z)$ e $(x.y).z=x.(y.z)$.
• Comutatividade: para quaisquer $x,y \in \mathbb{R}$ tem-se $x+y=y+x$ e $x.y=y.x$.
• Elementos neutros: Existem em $\mathbb{R}$ dois elementos distintos $0$ e $1$ tais que $x+0=x$ e $x.1=x$ para qualquer $x \in \mathbb{R}$.
• Inversos: todo $x \in \mathbb{R}$ possui um inverso aditivo $-x \in \mathbb{R}$ tal que $x+(-x)=0$ e, se $x\neq 0$, existe também um inverso multiplicativo $x^{-1} \in \mathbb{R}$ tal que $x.x^{-1}=1$.
• Distributividade: para quaisquer $x,y,z \in \mathbb{R}$ tem-se $x.(y+z)=x.y+x.z$.

Em outras palavras:

• Associatividade: na adição ou multiplicação de três números quaisquer, podemos adicionar o primeiro número com o segundo e em seguida, o seu resultado com o terceiro número. Da mesma forma com a multiplicação. Os parenteses indicam a ordem da primeira operação a ser realizada. Por exemplo:

Adição

$(2+3)+5=2+(3+5)$

$5+5=2+8$

$10=10$

Multiplicação

$(2.3).5=2.(3.5)$

$6.5=2.15$

$30=30$

• Comutatividade: a ordem das parcelas não altera o resultada da adição, assim como a ordem dos fatores não altera o produto na multiplicação. Por exemplo:

Adição

$1+2=2+1$

$3=3$

Multiplicação

$3.4=4.3$

$12=12$

• Elementos neutros: quaisquer números somados com $0$ o resultado sempre será o próprio número. Quaisquer números multiplicados por $1$, o produto sempre será o próprio número. Por exemplo:

Elemento neutro na Adição

$7+0=7$

$7=7$

Elemento neutro na Multiplicação

$7.1=7$

$7=7$

• Inversos: geralmente a palavra inversos é mais empregada na multiplicação e divisão. Seu significado para a Adição é de elemento simétrico ou oposto. Em resumo, a adição de dois números opostos resulta sempre em $0$. Já a multiplicação de dois números inversos resulta sempre em $1$. Por exemplo:

Inverso aditivo

$2+(-2)=0$

$2-2=0$

$0=0$

Inverso multiplicativo

$2.2^{-1}=1$

$2^{1+(-1)}=1$

$2^{0}=1$

$1=1$

• Distributividade: como o nome já sugere, é realizada a multiplicação do fator externo em relação as parcelas internas no parenteses. A multiplicação é a soma de parcelas iguais. Por isso a prioridade para a multiplicação. Por exemplo:

Distributividade da multiplicação em relação a adição

$2.(3+5)=2.3+2.5$

$2.8=6+10$

$16=16$

Outras propriedades surgem desses axiomas, como:

• Por que menos por mais é igual a menos? $(-x).(y)=x.(-y)=-(x.y)$; $\forall x\in \mathbb{R}$.
• Por que qualquer número multiplicado por zero é igual a zero? $\forall a\in \mathbb{R};a.0=0$
• Entre outras, mais conhecidas como "regras de sinais".

O que são fórmulas matemáticas?

Uma fórmula matemática pode surgir de um insight (uma intuição). Pode surgir de um experimento. Pode ser criada em consequência de outra fórmula. Toda fórmula matemática é verdadeira? Depende de uma demonstração rigorosa.

Uma fórmula matemática não é apenas uma expressão algébrica recheada de letras, números e símbolos. Dependendo de sua complexidade, ela trás conceitos simples e/ou abstratos, condições de existência e que necessita de pré-requisitos para compreendê-la e manuseá-la. A sua fluência em Matemática é importante para ler e compreender.

Fórmulas matemáticas devem ser demonstradas para que sejam aceitas como verdadeiras pela comunidade científica. Neste caso, uma comunidade mundial formada por matemáticos conceituados, verificam sua veracidade. Para provar que as fórmulas são verdadeiras ou não, os matemáticos utilizam técnicas rigorosas afim de demonstrar definitivamente se uma fórmula matemática (uma equação, inequação, etc.) está correta, tem falhas ou está totalmente errada. Algumas técnicas são:

• Prova direta: a conclusão é estabelecida através da combinação lógica dos axiomas, definições e teoremas já existentes.
• Prova por indução: um caso base é provado e uma regra de indução é usada para provar uma série de outros casos (normalmente infinita).
• Prova por contradição: é mostrado que se algum enunciado fosse verdadeiro, ocorreria uma contradição lógica, e portanto o enunciado deve ser falso.
• Prova por construção: consiste em construir um exemplo concreto com determinada propriedade para mostrar que existe algo com tal propriedade.
• Prova por exaustão: a conclusão é estabelecida dividindo o problema em um número finito de casos e provando cada um separadamente.
• Prova por força bruta: é o método que consiste em provar algum teorema (ou apresentar algum contra-exemplo) pelo método exaustivo de calcular cada caso possível.

A fórmula matemática mais linda na minha opinião está logo abaixo.

$e^{i.\pi}+1=0$
Veja um lindo wallpaper com essa fórmula

Em www.matematica.pt há uma lista de fórmulas matemáticas divididas em áreas como Trigonometria, Áreas de figuras planas, Volume, etc., todas escritas em Latex para facilitar o seu entendimento.

Dica de livro:

Título do livro: As grande equações - A história das fórmulas matemáticas mais importantes e os cientistas que as criaram. Compare os preços no Google Shopping.

Pré-requisitos para entender sobre fatorações

A Matemática básica estudada no Ensino Fundamental 2.

Atualização (21/12/17)

Para números racionais em $a$, $b$ e $c$ a fatoração pode se tornar mais trabalhosa. Nesse caso é recomendado calcular $\Delta$ pois ele pode ser negativo. Os exemplos citados nessa postagem se aplicada quando $a$, $b$ e $c$ são inteiros.

Aprenda a fatorar equações e esqueça de Bhaskara

Há um equívoco quanto ao nome que leva essa famosa fórmula. Esse costume de associar o nome de Bhaskara à fórmula, foi estabelecido no Brasil em meados da década de 60, e este fato é atribuído somente no Brasil.

Registros históricos indicam que os Babilônicos já usavam equações do 2º grau há aproximadamente 4 mil anos. (Mais sobre Bharkara e equação quadrática).

Não se trata de usar ou não usar essa fórmula para resolver equações do 2º grau, mas dos pré-requisitos matemáticos necessários que um estudante deve dominar, antes de fazer uso desse algoritmo.

Colocar a equação $x^{2}-5.x+6=0$, com $x\in \mathbb{R}$, no quadro e pedir para os alunos a resolverem usando $x=\cfrac{-b\pm \sqrt{b^{2}-4.a.c}}{2.a}$ é forçar demais, quando na verdade o correto seria mostrar como fatorá-la.

Dependendo do tipo (completa ou incompleta) da equação do 2º do grau, podemos calcular suas soluções apenas aplicando algumas propriedades de fatoração.

Forma de uma equação do 2º grau

A equação do 2º grau tem a seguinte a forma: $a.x^{2}+b.x+c=0$, com $x$, $a$, $b$ e $c \in \mathbb{R}$, sendo $a\neq 0$, pois caso contrário deixaria de ser uma equação de grau 2.

Desta forma temos algumas variações de equações quadráticas:

1. Quando $a \neq 0$, $b=0$ e $c \neq 0$; Exemplo: $4x^{2}-100=0$
2. Quando $a \neq 0$, $b \neq 0$ e $c=0$; Exemplo: $5x^{2}-25.x=0$
3. Quando $a \neq 0$, $b \neq 0$ e $c \neq 0$. Exemplo: $x^{2}-5.x+6=0$

Variação 1) Quando $a \neq 0$, $b=0$ e $c \neq 0$.

Como resolver a equação $4x^{2}-100=0$?

Solução:

Da mesma forma como resolvemos uma equação do 1º grau, bastando aplicar o Princípio Aditivo e Multiplicativo em ambos os membros. Assim:

$4x^{2}-100+(+100)=0+(+100)$ $\rightarrow$ Somando o oposto de $-100$ em ambos os membros (Princípio Aditivo)

$4x^{2}-100+100=0+100$

$4x^{2}+0=100$ $\rightarrow $ (Elementos simétricos)

$4x^{2}=100$ $\rightarrow $ (Elemento neutro da adição)

$\cfrac{1}{4}.4x^{2}=100.\cfrac{1}{4}$ $\rightarrow $ Multiplicando ambos os membros pelo inverso de $4$ (Princípio Multiplicativo)

$\cfrac{4x^{2}}{4}=\cfrac{100}{4}$

$x^{2}=25$

$\sqrt{x^{2}}=\sqrt{25}$ $\rightarrow $ Quadrando os dois membros da equação

$|x|=5$ $\rightarrow $ Simplificando a potência do radicando com o índice.

$x=5$ ou $x=-5$ $\rightarrow $ Por definição de módulo.

$S=\left \{-5;5 \right \}$

Aí você pergunta: pra que tudo isso? Essa é a teoria matemática que deve ser ensinada antes da aplicação da fórmula de Bhaskara. O domínio destas operações te trarão benefícios até mesmo para uma futura graduação.

Variação 2) Quando $a \neq 0$, $b \neq 0$ e $c=0$; Exemplo: $5x^{2}-25.x=0$

Para este caso, não há a necessidade mecânica de jogar os coeficiente desta equação na fórmula de Bhaskara. Use o processo matemático conhecido como Fator Comum e resolva a equação muito mais rápido e fácil do que com a fórmula.

Como o nome já sugere, é um termo algébrico que possui duas coisas em comum:

• Números múltiplos entre si (ou não);
• Variáveis semelhantes (destas, predomina o de menor expoente)

Neste exemplo, a equação $5x^{2}-25.x=0$ tem $5$ como fator comum, pois $5$ divide $5$ e $25$ ao mesmo tempo. E também temos $x$ (ou $x^{1}$) como sendo o fator comum entre $x^{2}$ e $x$. Logo, $5x$ é fator comum da equação. 

Desta forma podemos dividir a equação por $5x$ e assim, fatorá-la. Esse processo é mais conhecido como "colocar o termo em evidência".

Solução:

Como já explicado acima, $5x$ é o fator comum de $5x^{2}-25.x=0$. Logo, podemos efetuar a divisão da equação pelo termo em evidência - o monômio $5x$.

$5x^{2}-25.x=0$

$5x.(x-5)=0$ $\rightarrow $ $5x^{2}$ divido por $5x$ resulta em $x$ e $25x$ dividido por $5x$ resulta em $5$.

Após fatorar a equação em $5x.(x-5)=0$, aplique a propriedade de produto nulo. O que diz essa propriedade? Se $x.y=0$ $\Rightarrow$ $x=0$ ou $y=0$. Em outras palavras, só basta que um dos fatores seja $0$ (zero) para que o produto seja zero.

Portanto:

$5x.(x-5)=0$ $\Rightarrow$ $5x=0$ ou $(x-5)=0$

Agora temos duas equações do 1º grau. Aplicando os princípios aditivo e multiplicativo, encontramos a solução da equação.

$5x=0$

$x=0$

ou

$x-5=0$

$x=5$

$S=\left \{0;5 \right \}$

Esse método torna-se fácil, rápido e prático quando ele é compreendido e aplicado com muita frequência.

Variação 3) Quando $a \neq 0$, $b \neq 0$ e $c \neq 0$. Exemplo: $x^{2}+12.x+36=0$

Para esta variação de equação (completa) temos algumas formas diferentes para fazer a fatoração. Estas são as mais utilizadas:

1. Quadrado da soma ou diferença de dois termos: $(x+y)^{2}$ ou $(x-y)^{2}$
2. Trinômio quadrado perfeito: $x^{2}+2xy+y^{2}$
3. Soma e o produto da raízes: $S=\cfrac{-b}{a}$ e $P=\cfrac{c}{a}$. Os termos $a$, $b$ e $c$ são coeficientes de $a.x^{2}+b.x+c=0$.

Variação 3 - Caso 1

Para resolvermos uma equação do 2º grau completa na forma de quadrado da soma ou da diferença de dois termos, teremos que deixá-la assim: $(x+y)^{2}$ ou $(x-y)^{2}$.

Solução para $x^{2}+12.x+36=0$ usando $(x+y)^{2}$.

Note que $x^{2}+12.x+36=0$ é um trinômio quadrado perfeito (TQP), pois $x^{2}$ e $36$ são quadrados, $x$ e $6$ são suas bases e $12.x = 2.x.6$.

Desta forma: $x^{2}+2.x.6+6^{2}=(x+6)^{2}$ e portando escrevemos com um fator, apenas aplicando o conceito de potenciação.

Assim: $(x+6)^{2}=(x+6).(x+6)=0$. E agora aplicando o conceito de produto nulo, temos:

$(x+6)=0$ ou $(x+6)=0$
$x+6=0$
$x=-6$

ou

$x+6=0$
$x=-6$

$S=\{-6\}$

E quando o trinômio não for um quadrado perfeito? Vejamos o próximo caso.


Variação 3 - Caso 2

Basta aplicar o princípio aditivo para "montar" dois quadrados, e assim um trinômio quadrado perfeito.

Solução para $x^{2}-8.x+15=0$ usando o princípio aditivo.

Assim:

$x^{2}-8.x+15+(+1)=0+(+1)$ $\rightarrow $ Somando arbitrariamente $(+1)$ em ambos os membros da equação.
$x^{2}-8.x+16=1$ $\rightarrow $ Efetuado as adições normalmente.

Agora perceba que o primeiro membro $x^{2}-8.x+16=x^{2}-2.x.4+4^{2}$, ou seja, temos um trinômio quadrado perfeito. Perceba também que o segundo membro é $1$, que também é um quadrado perfeito. Logo a expressão $x^{2}-8.x+16=1$ está na forma $(n.x+m)^{2}=k$, com $x,n,m,k \in \mathbb{R}$ com $k\geqslant 0$.

Agora basta escrever $x^{2}-8.x+16=1$ como uma diferença de dois quadrados. Assim:

$x^{2}-8.x+16=1$
$x^{2}-2.x.4+4^{2}=1$
$(x-4)^{2}=1^{2}$
$(x-4)^{2}-1^{2}=0$

Note que $(x-4)^{2}-1^{2}=0$ é uma diferença entre dois quadrados, logo:

$[x-4+(+1)].[x-4+(-1)]=0$
$(x-3).(x-5)=0$

Aplique o princípio de produto nulo e encontrará a solução.

$x-3=0$ ou $x-5=0$

$x=3$ ou $x=5$

$S=\{3;5\}$.



Variação 3 - Caso 3

Solução para $x^{2}-8.x+15=0$ usando a soma e o produto das raízes da equação.

Soma das raízes: $S=\cfrac{-b}{a}$ e Produto das raízes: $P=\cfrac{c}{a}$

Os termos $a$, $b$ e $c$ são coeficientes de $a.x^{2}+b.x+c=0$. Os coeficientes de $x^{2}-8.x+15=0$ são: $a=1,$ $b=-8$ e $c=+15$.

Portanto, temos que: $S=\cfrac{-(-8)}{1}=8$ e $P=\cfrac{15}{1}=15$.

Temos que deixar $x^{2}-8.x+15=0$ na forma $x^2-S.x+P=0$, onde $S$ é a soma da raízes e $P$ é o produto das raízes.

Sendo assim, temos:

$x^2-S.x+P=0$ $\Rightarrow$ $x^{2}-(x_{1}+x_{2}).x+(x_{1}.x_{2})=0$. Ou seja, a soma das raízes tem que ser o oposto do coeficiente de $b$ (no caso $8$) e o produto das raízes tem que ser igual ao coeficiente de $c$ (no caso $15$).

Isso implica que a fatoração deverá ficar assim: $a.(x-x_{1}).(x-x_{2})=0$ (Relação de Girard), com $a\neq 0,$ e $x_{1},$ $x_{2}$ são as raízes.

Para fatorar $x^{2}-8.x+15=0$, fazemos:

$1.[x-(+3)].[(x-(+5)]=0$, pois $(+3).(+5)=15$ ($P$) e $(+3)+(+5)=+8$ ($S$ oposto de $b$).

$(x-3).(x-5)=0$

Aplique o princípio de produto nulo e encontrará a solução.

$x-3=0$ ou $x-5=0$

$x=3$ ou $x=5$

$S=\{3;5\}$.

Parece complicado à primeira vista, pois você está tentando entender mediante uma leitura. Também não sabia resolver equações usando a fatoração. Tive que ler e praticar muito para obter mais habilidade com esses cálculos.

Na época que estudava equações e funções quadráticas no Ensino Médio, o professor não se preocupava se ensinava da forma correta ou se a turma entendia algo. Conto essa história completa no artigo Como treinei meu cérebro para me tornar fluente em Matemática.

Nele relato minha experiência com a aprendizagem de cálculos matemáticos no Ensino Fundamental, Médio e Superior. Aproveite e leia os comentários, tem muita gente semelhante a você que acha que não pode aprender Matemática. Se inspire e lute por aquilo que deseja.

Concluindo

Existem diversas formas de fatorar equações do 2º grau sem usar Bhaskara. As abordadas neste artigo são as mais vistas nas aulas de Matemática. Elas dependem muito de diversos processos que antecedem a fatoração. Tentar aprendê-los sem antes de uma revisão minuciosa, terá mais dificuldades para absorver.

Este artigo não tem a intenção de induzir você a esquecer a aplicação da fórmula de Bhaskara ou de qualquer outra fórmula matemática, para resolver equações do 2º grau.

O que pretendo é apenas não se limitar ao uso de fórmulas. Elas são lindas, aplicáveis e o mundo moderno de hoje não suportaria viver sem ela, porém, em processos matemáticos do 6º ano do Ensino Fundamental ao Ensino Superior, o que mais vemos são elas.

Uma coisa é entendê-la e usá-la de forma correta e aplicável. Outra coisa totalmente diferente é jogá-la no quadro pela primeira vez e pedir para nossos alunos substituir alguns coeficientes e resolvê-la sem nenhum ponto de observação, abstração e pensamento matemático.